The source code implementing the projections below is only available on request for a small fee. It includes a demo application and an invitation to convert an image of your choice to verify the code does what you seek. For more information please contact the author.

Introduction

The following presents one method by which two fisheye images, with sufficient apertures, can be combined to form one spherical (equirectangular) projection. It is one of two main approaches, this is a purely geometric algorithm, the alternative is to detect feature points between the two overlapping fisheye images and perform a warp/blend.

A "fisheye" image is taken to mean a projection defined as a circular fisheye, namely radially symmetric in longitude and with latitude proportional to the radius from the center of the fisheye circle. Most lenses do have some non-linearity and this is a relatively straightforward correction to make. A fisheye is defined for any angle, 180 being the most common but in the context here one requires greater than 180 degrees. The fisheye circle may be smaller than the image frame it is contained in (sensor size) or it may be larger, so the circle is clipped. Both these situations are common for real fisheye images and camera sensors and as such need to be dealt with.

The algorithm described here is tested with a command line utility that accepts various command line option and reads a parameter file describing attributes of the fisheye images. The usage string is as follows.

Usage: dualfish2sphere [options] parameterfile
Options
   -w n    sets the output image size, default: twice fisheye width
   -a n    sets antialiasing level, default: 2
   -b n    longitude width for blending, default: no blending
   -d      debug mode

The algorithm, as with many of this nature, considers each pixel in the output image and determines the best estimate from the input images. Antialising here is performed using a simple supersampling approach, each pixel in the output image is sampled multiple times at different subpixel positions, the best estimates from the input images are averaged together. For fisheye images greater than 180 degree aperture, the two overlapping halves of their projection into equirectangular space are blended together using a simple linear multiplicative blend function.

The parameter file consists of a series of lines consisting of a keyword and value pair. At the very least the file must contain two IMAGE: keywords, the modifier keywords can appear in any order and apply to the previously defined IMAGE:. Noting that the order in which the rotate keywords appear determines the order in which they are performed. An example parameter file is given below, the meanings of the keywords should be clear. A line starting with a "#" is a comment line, the rest of the line will be ignored. All angles are defined in degrees and all coordinates are defined in pixels.

# left image
IMAGE: sample.tga
RADIUS: 904
CENTER: 959 970
APERTURE: 190
ROTATEZ: -1.2
ROTATEX: 0
ROTATEY: -90
# right image
IMAGE: sample.tga
RADIUS: 904
CENTER: 2879 948
APERTURE: 189
ROTATEX: -2
ROTATEY: 90

In the above the two fisheye images are assumed to be in the same image, one on the left of the other although the algorithm isn't affected by the order. The software also handles the case where the two fisheyes are located within different files. CENTER: defines the center of the fisheye circle (origin is the top left corner of the image). RADIUS: is the radius of the fisheye circle that matches the given APERTURE:. The conventions for a single file containing two fisheye images is given below.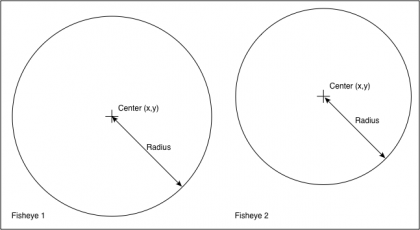

Note the extreme generality of these defining parameters, the fisheye images need not have the same aperture, radius, or position in the image. This is largely to deal with integrated dual fisheye systems that, in the real world, are rarely perfect. For example the lenses are not always on the same optical axis and there is variation between the optics of any two fisheye lenses.

The various rotation angles provide a mechanism by which corrections can be made to the fisheye camera/lens system, for example if they don't share the same optical axis. The fisheye lens/camera is assumed to be looking down the y axis, so ROTATEY: serves to roll the fisheye. The x axis is assumed to be to the right, so a ROTATEX serves to correct for the fisheye tilt. The z axis is up so ROTATEZ: serves to pan the fisheye. Note the since the algorithm operates in reverse (from the output image to the input fisheye) the rotational transformations act in the reverse order to which they appear in the parameter file.

The following example will illustrate the main features of the algorithm implementation. It will be based upon two separate fisheye images, each with an aperture of 210 degrees.

In this somewhat artificial example the left fisheye above is tilted up by 10 degrees. The right fisheye above is rotated clockwise off the optical axis by 5 degrees. The parameter file is given below.

# Example for online example
# first fisheye
IMAGE: exampleleft.tga
APERTURE: 210
RADIUS: 1024
CENTER: 1024 1124
ROTATEX: -10
# second fisheye
IMAGE: exampleright.tga
CENTER: 1124 1024
RADIUS: 1024
APERTURE: 210
ROTATEY: -5

Each fisheye is located in a different part of the image (sensor) plane. The resulting panorama after compensating correctly for these camera/fisheye errors is shown below.

So how does this work? Each fisheye, assuming it has an aperture of at least 180 degrees captures half the visible world, another fisheye pointing in the opposite direction captures the other half. It should therefore be possible to merge the two fisheye images together to form a complete equirectangular projection, which defines the whole visible world. The left fisheye above mapped into equirectangular space is shown below, it fills more than half the equirectangular image because the lens is 210 degrees. Some additional notes and implementation of converting fisheye to equirectangular images can be found here.

Repeating for the right hand fisheye above gives the following, noting that it generally covers the second half of the equirectangular image and in this case is continuous across the 0 to 360 agle wrap.

As long as the fisheyes have an aperture greater than 180 degrees there is some image overlap to blend the two halves together. The two images with a blend zone of 15 degrees (75 degrees to 105 degrees) are given below. The final image is achieved by simply adding these on a pixel by pixel basis.

Notes

• Fisheye angles of 190 degrees or more are required for a satisfactory blend zone, 10 degrees.

• The discussion here does not address the fundamental issues of parallax error in real dual fisheye systems where the nodal points do now coincide. A perfect blend can occur at any one distance but not at all distances.